How To Draw The Incenter Of A Triangle

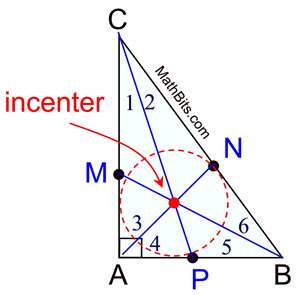
The angle bisectors of the angles of a triangle are concurrent (they intersect in one common bespeak). The betoken of concurrency of the angle bisectors is called the incenter of the triangle. The point of concurrency is always located in the interior of the triangle.

NOTE: The bespeak of concurrency of the angle bisectors of a triangle (the incenter) is the center of an inscribed circle inside the triangle.

An inscribed circle is a circumvolve positioned within a figure such that the circumvolve is tangent to each of the sides of the figure. In this case, the circle is tangent to the sides of the triangle. A circumvolve is tangent to a segment (or line) if it touches the segment only once, only does not cross the segment. Since radii in a circumvolve are of equal length, the incenter is equidistant from the sides of the triangle.

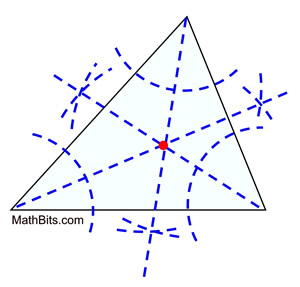
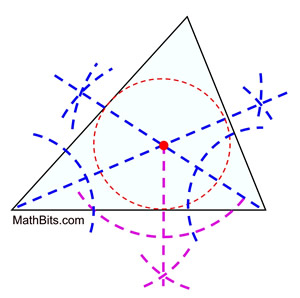
Locate the incenter through construction: We have seen how to construct angle bisectors of a triangle. Simply construct the angle bisectors of the three angles of the triangle. The point where the bending bisectors intersect is the incenter. Actually, finding the intersection of only 2 angle bisectors will find the incenter. Finding the third angle bisector, however, will ensure more accurateness of the notice.
Construct a circle inscribed in a triangle. When we circumscribed a circle about a triangle, we determined the radius of the circumvolve by measuring the distance from the eye to a vertex. When constructing an inscribed triangle, nosotros tin "eyeball" the radius of our circle, but we have no actual length to measure. We demand a length, since "eyeballing" is not sufficient. To determine the length, nosotros volition construct a perpendicular to one side from the heart bespeak to locate the radius. Theorem: The radius of a circle drawn to the point of tangency of a tangent line is perpendicular to the tangent.
Steps: 1. locate the incenter by constructing the bending bisectors of at to the lowest degree two angles of the triangle. 2. construct a perpendicular from the incenter to one side of the triangle to locate the exact radius. 3. place compass indicate at the incenter and measure from the center to the point where the perpendicular crosses the side of the triangle (the radius of the circumvolve). 4. describe the circle.